一、PID简介
PID控制是自动控制系统中最常用的一种控制手段，它的诞生主要是为了解决自动控制系统的快、稳、准的问题。
PID控制中的P指的是Proportion（比例），即对输入的偏差乘以一个系数；I指的是Integral（积分），即对输入偏差进行积分运算；而D指的是Derivative（微分），即对输入偏差进行微分运算。通过比例、积分、微分结合适当的反馈就可以形成一套稳定的闭环调节系统。如下图所示为COCOFLY的PID控制器的结构图。
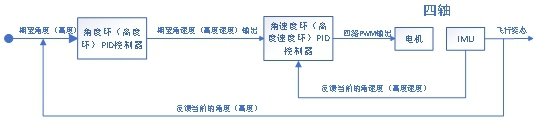
其中期望角度（高度）由遥控器提供，角度环（高度环）以及角速度环（高速度环）由PID代码处理，STM32输出四路PWM到无人机的电机控制端口，IMU（惯性测量单元）以及飞行姿态提供反馈值。
二、PID控制原理
PID控制的过程，其实是不断纠正偏差的过程，其中的偏差=当前被控对象的反馈值-设定的期望值。
这里举一个比较简单又经典的PID控制的例子，比如需要控制一个机器人以PID的方式向前行走110步，然后停下来。此时这个110步则是设定的期望值。
如果按照P比例控制，也就是控制机器人按照一定的比例走，然后停下。比如比例系数为108，则走一次就走了108步，再走一次的话就超过110步了，所以就不走了。从这里可得知P比例控制是一种最简单的控制方式，控制器的输出与输入误差信号成比例关系。但是仅有比例控制时系统输出存在稳态误差。比如上面的只能走到108，或者超过108步，无论怎样都走不到110。
为了消除稳态误差，在控制器中必须引入“积分项I”。积分项对误差的影响取决于时间的积分，随着时间的增加，积分项会增大。这样，即便误差很小，积分项也会随着时间的增加而加大，它推动控制器的输出增大，从而使稳态误差进一步减小，直到等于0。即在“积分项I”控制中，控制器的输出与输入误差信号成正比关系，且比例+积分（PI）控制器可以使系统在进入稳态后无稳态误差。
也就是说，如果按照PI（比例、积分）控制的方式，则是控制机器人按照一定的步伐走到112步然后回头接着走，走到108步位置时，然后又回头向110步位置走。在110位置处来回晃荡几次，最后停在110步的位置。
微分项，主要用于预判误差变化的趋势从而作出对应的改变。在自动控制系统在克服误差的调节过程中可能会出现振荡甚至失稳，原因是存在较大惯性组件（环节）或滞后组件，具有抑制误差的作用，其变化总是落后于误差的变化。解决的办法是使抑制误差作用的变化“超前”，即在误差接近于零时，抑制误差的作用就应该是零。这就是说，在控制器中仅引入“比例P”项往往是不够的，比例项的作用仅是放大误差的幅值，而目前需要增加的是“微分项”，它能预测误差变化的趋势。这样，具有比例+微分的控制器就能够提前使抑制误差的控制作用等于零，甚至为负值，从而避免了被控量的严重超调。所以对有较大惯性或滞后的被控对象，比例P+微分D（PD）控制器能改善系统在调节过程中的动态特性。
也就是说，如果按照PD比例、微分控制的方式，则为控制机器人按照一定的步伐走到一百零几步后，再慢慢地走向110步的位置靠近，如果最后能精确停在110步的位置，就是无静差控制；如果停在110步附近（如109步或111步位置），就是有静差控制。由此得知在微分控制D中，控制器的输出与输入误差信号的微分（即误差的变化率）成正比关系。
前面说到PID是为了解决自动控制系统中的快、稳、准的问题的。其中那么他们之间的关系以及对应调节参数是什么呢？如下表所示。
|
特性
|
概述
|
关联的参数
|
|
快速性
|
系统对动态响应的要求，由响应时间的长短来衡量。
|
P和D可以提高响应速度，I降低响应速度。
|
|
稳定性
|
在平衡状态下，系统受到某个干扰后，经过一段时间其被控量可以达到某一稳定状态。
|
P和I降低系统稳定性，D提高系统稳定性。
|
|
准确性
|
系统处于稳态时，其稳态误差。
|
P和I提高稳态精度，D无作用
|
三、PID代码结构
在飞控系统中PID是极为重要的一环，在COCOFLY飞控系统中也多处应用到了PID主要集中在AltCtrl.c、Ctrl.c中。如下图所示为高度环PID控制源码。
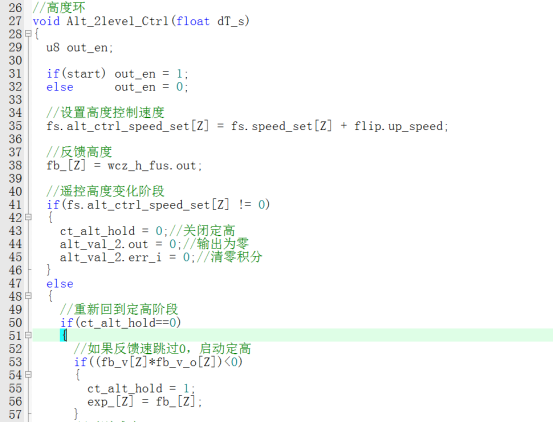
如下图所示为高度速度环PID控制源码。
如下图所示为角度环PID控制源码。
如下图所示为角速率环PID控制源码。
提升卡
变色卡
千斤顶
1/9 
京公网安备 11010802033920号
Copyright © 2005-2025 EEWORLD.com.cn, Inc. All rights reserved
